| Designing Secure Software by Loren Kohnfelder (all rights reserved) |
|---|
| Home 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 Appendix: A B C D |
| Buy the book here. |
“Cryptography is typically bypassed, not penetrated.” —Adi Shamir
Back in high school, I nearly failed driver’s education. This was long ago, when public schools had funding to teach driving, and when gasoline contained lead (nobody had threat modeled that brilliant idea). My first attempts at driving had not gone well. I specifically recall the day I first got behind the wheel of the Volkswagen Beetle, a manual transmission car, and the considerable trepidation on the stony face of the PE coach riding shotgun. I soon learned that pushing in the clutch while going downhill caused the car to speed up, not slow down as I’d intended. But from that mistake onward, something clicked, and suddenly I could drive. The coach expressed unguarded surprise, and relief, at this unlikely turn of events. With hindsight, I believe that my breakthrough was due to the hands-on feel of driving stick, which gave me a more direct connection to the vehicle, enabling me to drive by instinct for the first time.
Just as driver’s ed teaches students how to drive a car safely, this chapter introduces the basic toolset of cryptography by discussing how to use it properly, without going into the nuts and bolts of how it works. To make crypto comprehensible to the less mathematically inclined, this chapter eschews the math, except in one instance, whose inclusion I couldn’t resist because it’s so clever.
This is an unconventional approach to the topic, but also an important one. Crypto tools are underutilized precisely because cryptography has come to be seen as the domain of experts with a high barrier of entry. Modern libraries provide cryptographic functionality, but developers need to know how to use these (and how to use them correctly) for them to be effective. I hope that this chapter serves as a springboard to provide useful intuitions about the potential uses of crypto. You should supplement this with further research, as needed for your specific uses.
Crypto Tools
At its core, much of modern crypto derives from pure mathematics, so when used properly, it really works. This doesn’t mean the algorithms are provably impenetrable, but that it will take major breakthroughs in mathematics to crack them.
Crypto provides a rich array of security tools, but for them to be effective, you must use them thoughtfully. As this book repeatedly recommends, rely on high-quality libraries of code that provide complete solutions. It’s important to choose a library that provides an interface at the right level of abstraction, so you fully understand what it is doing.
The history of cryptography and the mathematics behind it are fascinating, but for the purposes of creating secure software, the modern toolbox consists of a modest collection of basic tools. The following list enumerates the basic crypto security functions and describes what each does, as well as what the security of each depends on:
- Random numbers are useful as padding and nonces, but only if they are unpredictable.
- Message digests (or hash functions) serve as a fingerprint of data, but only if impervious to collisions.
- Symmetric encryption conceals data based on a secret key the parties share.
- Asymmetric encryption conceals data based on a secret the recipient knows.
- Digital signatures authenticate data based on a secret only the signer knows.
- Digital certificates authenticate signers based on trust in root certificate.
The rest of this chapter will cover these tools and their uses in more detail.
Random Numbers
Human minds struggle to grasp the concept of randomness. For security purposes, we can focus on unpredictability as the most important attribute of random numbers. As we shall see, these are critical where we must prevent attackers from guessing correctly, just as a predictable password would be weak. Applications for random numbers include authentication, hashing, encryption, and key generation, each of which depends on unpredictability. The following subsections describe the two classes of random numbers available to software, how they differ in predictability, and when to use which kind.
Pseudo-Random Numbers
Pseudo-random number generators (PRNGs*)* use deterministic computations to produce what looks like an infinite sequence of random numbers. The outputs they generate can easily exceed our human capacity for pattern detection, but analysis and adversarial software may easily learn to mimic a PRNG, disqualifying these from use in security contexts because they are predictable.
However, since calculating pseudo-random numbers is very fast, they’re ideal for a broad range of non-security uses. If you want to run a Monte Carlo simulation, or randomly assign variant web page designs for A/B testing, for example, a PRNG is the way to go, because even in the unlikely event that someone predicts the algorithm there’s no real threat.
Taking a look at an example of a pseudo-random number may help solidify your understanding of why it is not truly random. Consider this digit sequence:
94657640789512694683983525957098258226205224894077267194782684826
Is this sequence random? There happen to be relatively few 1s and 3s, and
disproportionally many 2s, but it wouldn’t be unreasonable to find these
deviations from a flat distribution in a truly random number. Yet as random as
this sequence appears, it’s easy to predict the next digits if you know the
trick. And as the pattern of Transparent Design cautions us, it’s risky to
assume we can keep our methods secret. In fact, if you entered this string of
digits in a simple web search, you would learn that they are the digits of pi
200 decimals out, and that the next few digits will be 0147.
As the decimals of an irrational number, the digits of pi have a statistically normal distribution and are, in a colloquial sense, entirely random. On the other hand, as an easily computed and well-known number, this sequence is completely predictable, and hence unsuitable for security purposes.
Cryptographically Secure Pseudo-Random Numbers
Modern operating systems provide cryptographically secure** pseudo-random number generator (CSPRNG) functions to address the shortcomings of PRNGs when you need random bits for security. You may also see this written as CSRNG or CRNG; the important part is the “C,” which means it’s secure for crypto. The inclusion of “pseudo” is an admission that these, too, may fall short of perfect randomness, but experts have deemed them unpredictable enough to be secure for all practical purposes.
Use this kind of random number generator when security is at stake. In other words, if the hypothetical ability to predict the value of a supposedly random number weakens your security, use a CSPRNG. This applies to every security use of random numbers mentioned in this book.
Truly random data, by definition, isn’t generated by an algorithm, but comes from an unpredictable physical process. A Geiger counter could be such a hardware random number generator (HRNG), also known as an entropy source, because the timing of radioactive decay events is random. HRNGs are built into many modern processors, or you can buy a hardware add-on. Software can also contribute entropy, usually by deriving it from the timing of events such as disk accesses, keyboard and mouse input events, and network transmissions that depend on complex interactions with external entities.
One major internet tech company uses an array of lava lamps to colorfully generate random inputs. But consider a threat model of this technique: because the company chooses to display these lava lamps in its corporate office, and in the reception area no less, potential attackers might be able to observe the state of this input and make an educated guess about the entropy source. In practice, however, the lava lamps merely add entropy to a (presumably) more conventional entropy source behind the scenes, mitigating the risk that this display will lead to an easy compromise of the company’s systems.
Entropy sources need time to produce randomness, and a CSPRNG will slow down to a crawl if you demand too many bits too fast. This is the cost of secure randomness, and why PRNGs have an important purpose as a reliably fast alternative. Use CSPRNGs sparingly unless you have a fast HRNG, and where throughput is an issue, test that it won’t become a bottleneck.
Message Authentication Codes
A message digest (also called a hash) is a fixed-length value computed from a message using a one-way function. This means that each unique message will have a specific digest, and any tampering will result in a different digest value. Being one-way is important because it means the digest computation is irreversible, so it won’t be possible for an attacker to find a different message that happens to have the same digest result. If you know that the digest matches, then you know that the message content has not been tampered with.
If two different messages produce the same digest, we call this a collision. Since digests map large chunks of data to fixed-length values, collisions are inevitable because there are more possible messages than there are digest values. The defining feature of a good digest function is that collisions are extremely difficult to find. A collision attack succeeds if an attacker finds two different inputs that produce the same digest value. The most devastating kind of attack on a digest function is a preimage attack, where, given a specific digest value, the attacker can find an input that produces it.
Cryptographically secure digest algorithms are strong one-way functions that make collisions so unlikely that you can assume they never happen. This assumption is necessary to leverage the power of digests because it means that by comparing two digests for equality, you are essentially comparing the full messages. Think of this as comparing two fingerprints (which is also an informal term for a digest) to determine if they were made by the same finger.
If everyone used the same digest function for everything then attackers could intensively study and analyze it, and they might eventually find a few collisions or other weaknesses. One way to guard against this is to use keyed hash functions, which take an extra secret key parameter that transforms the digest computation. In effect, a keyed hash function that takes a 256-bit key is a class of 2^256 different functions. These functions are also called message authentication codes (MACs), because so long as the hash function key is secret, attackers cannot forge them. That is, by using a unique key, you get a customized digest function all your own.
Using MACs to Prevent Tampering
MACs are often used to prevent attackers from tampering with data. Suppose Alice wants to send a message to Bob over a public channel. The two of them have privately shared a certain secret key; they don’t care about eavesdropping, so they don’t need to encrypt their data, but fake messages would be a problem if undetected. Say the evil Mallory is able to tamper with communications on the wire, but she does not know the key. Alice uses the key to compute and send a MAC along with each message. When Bob receives a communication, he computes the MAC of the received message and compares it to the accompanying MAC that Alice sent; if they don’t match, he ignores it as bogus.
How secure is this arrangement at defending against the clever Mallory? First, let’s consider the obvious attacks:
- If Mallory tampers with the message, its MAC will not match the message digest (and Bob will ignore it).
- If Mallory tampers with the MAC, it won’t match the message digest (and Bob will ignore it).
- If Mallory concocts a brand-new message, she will have no way to compute the MAC (and Bob will ignore it).
However, there is one more case that we need to protect against. Can you spot another opening for Mallory, and how you might defend against it?
Replay Attacks
There is a remaining problem with the MAC communication scheme described previously, and it should give you an idea of how tricky using crypto tools against a determined attacker is. Suppose that Alice sends daily orders to Bob indicating how many widgets she wants delivered the next day. Mallory observes this traffic and collects message and MAC pairs that Alice sends: she orders three widgets the first day, then five the next. On the third day, Alice orders 10 widgets. At this point, Mallory gets an idea of how to tamper with Alice’s messages. Mallory intercepts Alice’s message and replaces it with a copy of the first day’s message (specifying three widgets), complete with the corresponding MAC that Alice has helpfully computed already and which Mallory recorded earlier.
This is a replay attack, and secure communications protocols need to address it. The problem isn’t that the cryptography is weak, it’s that it wasn’t used properly. In this case, the root problem is that authentic messages ordering three widgets are identical, which is fundamentally a predictability problem.
Secure MAC Communications
There are a number of ways to fix Alice and Bob’s protocol and defeat replay attacks, and they all depend on ensuring that messages are always unique and unpredictable. A simple fix might be for Alice to include a timestamp in the message, with the understanding that Bob should ignore messages with old timestamps. Now if Mallory replays Monday’s order of three widgets on Wednesday, Bob will notice when he compares the timestamps and detect the fraud. If the messages are frequent, or there’s a lot of network latency, however, timestamps might not work well.
A better solution to the threat of replay attacks would be for Bob to send Alice a nonce—a random number for one-time use—before Alice sends each message. Then Alice can send back a message along with Bob’s nonce and a MAC of the message and nonce combined. This shuts down replay attacks, because the nonce varies with every exchange. Mallory could intercept and change the nonce Bob sends, but Bob would notice if a different nonce came back.
Another problem with this simple example is that the messages are short, consisting of just a number of widgets. Setting aside the danger of replay attacks, very short messages are vulnerable to brute-force attacks. The time required to compute a keyed hash function is typically proportional to the message data length, and for just a few bits that computation is going to be fast. The faster Mallory can try different possible hash function keys, the easier it is to guess the right key to match the MAC of an authentic message. Knowing the key, Mallory can now impersonate Alice sending messages.
You can mitigate short message vulnerabilities by padding the messages with random bits until they reach a suitable minimum length. Computing the MACs for these longer messages takes time, but that’s good as it slows down Mallory’s brute-force attack to the point of being infeasible. In fact, it’s desirable for hash functions to be expensive computations for just this reason. This is a situation where it’s important for the padding to be random (as opposed to predictably pseudo-random) to make Mallory work as hard as possible.
Symmetric Encryption
All encryption conceals messages by transforming the plaintext, or original message, into an unrecognizable form called the ciphertext. Symmetric encryption algorithms use a secret key to customize the message’s transformation for the private use of the communicants, who must agree on a key in advance. The decryption algorithm uses the same secret key to convert ciphertext back to plaintext. We call this reversible transformation symmetric cryptography because knowledge of the secret key allows you to both encrypt and decrypt.
This section introduces a couple of these symmetric encryption algorithms to illustrate their security properties, and explains some of the precautions necessary to use them safely.
One-Time Pad
Cryptographers long ago discovered the ideal encryption algorithm, and even though, as we shall see, it is almost never actually used, it’s a great starting point for discussing encryption due to its utter simplicity. Known as the one-time pad, this algorithm requires the communicants to agree on a secret, random string of bits as the encryption key in advance. In order to encrypt a message, the sender exclusive-ors the message with the key, creating the ciphertext. The recipient then exclusive-ors the ciphertext with the same corresponding key bits to recover the plaintext message. Recall that in the exclusive-or (⊕) operation, if the key bit is a zero, then the corresponding message bit is unchanged; if the key bit is a one, then the message bit is inverted. Figure 5-1 graphically illustrates a simple example of one-time pad encryption and decryption.
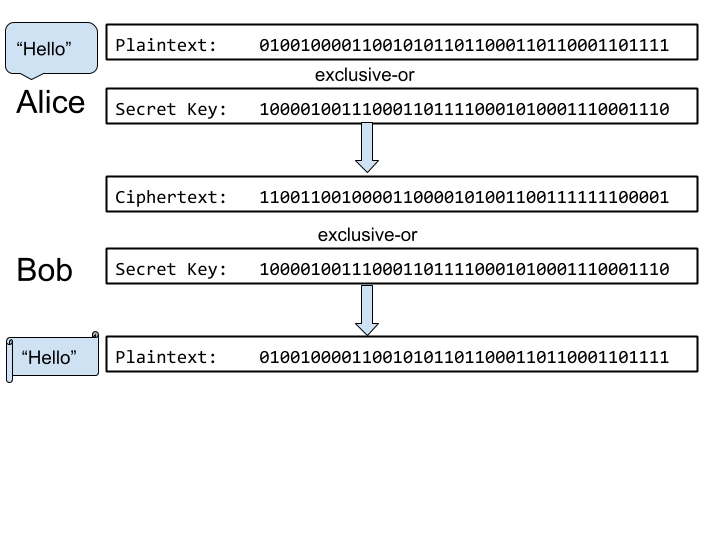
Figure 5-1 Alice and Bob using one-time pad encryption
Subsequent messages are encrypted using bits further along in the secret key bit string. When the key is exhausted, the communicants need to somehow agree on a new secret key. There are good reasons it’s a one-time key, as I will explain shortly. Assuming that the key is random, the message bits either randomly invert or not, so there is no way for attackers to discern the original message without knowing the key. Flipping exactly half the bits randomly is the perfect disguise for a message, since either showing or inverting a large majority of the bits would partially reveal the plaintext. Impervious to attack by analysis as this may be, it’s easy to see why this method is rarely used: the key length limits the message length.
Let’s consider the prohibition against reusing one-time pad keys. Suppose that
Alice and Bob use the same secret key K to encrypt two distinct plaintext
messages, M1 and M2. Mallory intercepts both ciphertexts: (M1 ⊕ K) and
(M2 ⊕ K). If Mallory exclusive-ors the two encrypted ciphertexts, the key
cancels out, because when you exclusive-or any number with itself the result is
zero (the ones invert to zeros, while the zeros are unchanged). The result is a
weakly encrypted version of the two messages:
(M1 ⊕ K) ⊕ (M2 ⊕ K) = (M1 ⊕ M2) ⊕ (K ⊕ K) = M1 ⊕ M2
While this doesn’t directly disclose the plaintext, it begins to leak information. Having stripped away the key bits, analysis could reveal clues about patterns within the messages. For example, if either message contains a sequence of zero bits, then the corresponding bits of the other message will leak through.
The one-time key use limitation is a showstopper for most applications: Alice and Bob may not know how much data they want to encrypt in advance, making deciding on a key length infeasible.
Advanced Encryption Standard
The Advanced Encryption Standard (AES) is a frequently used modern symmetric encryption block cipher algorithm. In a block cipher, long messages are broken up into block-sized chunks, and shorter messages are padded with random bits to fill out the remainder of the block. AES encrypts 128-bit blocks of data using a secret key that is typically 256 bits long. Alice uses the same agreed-upon secret key to encrypt data that Bob uses to decrypt.
Let’s consider some possible weaknesses. If Alice sends identical message blocks to Bob over time, these will result in identical ciphertext, and clever Mallory will notice these repetitions. Even if Mallory can’t decipher the meaning of these messages, this represents a significant information leak that requires mitigation. The communication is also vulnerable to a replay attack, because if Alice can resend the same ciphertext to convey the same plaintext message, then Mallory could do that, too.
Encrypting the same message in the same way is known as electronic code book (ECB) mode. Because of the vulnerability to replay attacks, this is usually a poor choice. To avoid this problem, you can use other modes that introduce feedback or other differences into subsequent blocks, so that the resulting ciphertext depends on the contents of preceding blocks or the position in the sequence. This ensures that even if the plaintext blocks are identical, the ciphertext results will be completely different. However, while chained encryption of data streams in blocks is advantageous, it does impose obligations on the communicants to maintain context of the ordering to encrypt and decrypt correctly. The choice of encryption modes thus often depends on the particular needs of the application.
Using Symmetric Cryptography
Symmetric crypto is the workhorse for modern encryption because it’s fast and secure when applied properly. Encryption protects data communicated over an insecure channel, as well as data at rest in storage. Before starting, it’s important to consider some fundamental limitations:
– Key establishment — Crypto algorithms depend on the prearrangement of secret keys, but do not specify how these keys should be established.
– Key secrecy — The effectiveness of the encryption entirely depends on maintaining the secrecy of the keys while still having the keys available when needed.
– Key size — Larger secret keys are stronger (with a one-time pad being the ideal in theory), but managing large keys becomes costly and unwieldy.
Symmetric encryption inherently depends on shared secret keys, and unless Alice and Bob can meet directly for a trusted exchange, it’s challenging to set up. To address this limitation, asymmetric encryption offers some surprisingly useful new capabilities that fit the needs of an internet-connected world.
Asymmetric Encryption
Asymmetric cryptography is a deeply counterintuitive form of encryption, and therein lies its power. With symmetric encryption Alice and Bob can both encrypt and decrypt messages using the same key, but with asymmetric encryption Bob can send secret messages to Alice that he is unable to decrypt. Thus, for Bob encryption is a one-way function, while only Alice knows the secret that enables her to invert the function (that is, to decrypt the message).
Asymmetric cryptography uses a pair of keys: a public key for encryption, and a private key for decryption. I will describe how Bob, or anyone in the world for that matter, sends encrypted messages to Alice; for a two-way conversation, Alice would reply using the same process with Bob’s entirely separate key pair. The transformations made using the two keys are inverse functions, yet knowing only one of the keys does not help to figure out the other, so if you keep one key secret then only you can perform that computation. As a result of this asymmetry, Alice can create a key pair and then publish one key for the world to see (her public key), enabling anyone to encrypt messages that only she can decrypt using her corresponding private key. This is revolutionary, because it grants Alice a unique capability based on knowing a secret. We shall see in the following pages all that this makes possible.
There are many asymmetric encryption algorithms, but the mathematical details of these are unimportant to understanding using them as crypto tools—what’s important is that you understand the security implications. We’ll focus on RSA, as it’s the least mathematically complicated progenitor.
The RSA Cryptosystem
At MIT, I had the great fortune to work with two of the inventors of the RSA cryptosystem, and my bachelor’s thesis explored how asymmetric cryptography could improve security. The following simplified discussion follows the original RSA paper, though (for various technical reasons that we don’t need to go into here) modern implementations are more involved.
The core idea of RSA is that it’s easy to multiply two large prime numbers together, but given that product, it’s infeasible to factor it into the constituent primes. To get started, choose a pair of random large prime numbers, which you will keep secret. Next, multiply the pair of primes together. From the result, which we’ll call N, you can compute a unique key pair. Each of these keys, together with N, allows you compute two functions D and E that are inverse functions. That is, for any positive integer x < N, D(E(x)) is x, and E(D(x)) is also x. Finally, choose one of the keys of the key pair as your private key, and publicize to the world the other as the corresponding public key, along with N. So long as you keep the private key and the original two primes secret, only you can efficiently compute the function D.
Here’s how Bob encrypts a message for Alice, and how she decrypts it. Here the functions EA and DA are based on Alice’s public and private keys, respectively, along with N:
- Bob encrypts a ciphertext C from message M for Alice using her public key: C = EA(M).
- Alice decrypts message M from Bob’s ciphertext C using her private key: M = DA(C).
Since the public key is not a secret, we assume that the attacker Mallory knows it, and this does raise a new concern particular to public key crypto. If an eavesdropper can guess a predictable message, they can encrypt various likely messages themselves using the public key and compare the results to the ciphertext transmitted on the wire. If they ever see matching ciphertext transmitted, they know the plaintext that produced it. Such a chosen plaintext attack is easily foiled by padding messages with a suitable number of random bits to make guessing impractical.
RSA was not the first published asymmetric cryptosystem, but it made a big splash because cracking it (that is, deducing someone’s private key from their public key) requires solving the well-known hard problem of factoring the product of large prime numbers. Since I was collaborating in a modest way with the inventors of RSA at the time of its public debut, I can offer a historical note that may be of interest about its significance then versus now. The algorithm was too compute-intensive for the computers of its day, so its use required expensive custom hardware. As a result, we envisioned it being used only by large financial institutions or military intelligence agencies. We knew about Moore’s law, which proposed that computational power increases exponentially over time—but nobody imagined then that 40 years later everyday people would routinely use connected mobile smartphones with processors capable of doing the necessary number crunching!
Today, RSA is being replaced by newer methods such as elliptic curve algorithms. These algorithms, which rely on different mathematics to achieve similar capabilities, offer more “bang for the buck,” producing strong encryption with less computation. Since asymmetric crypto is typically more computationally expensive than symmetric crypto, encryption is usually handled by choosing a random secret key, asymmetrically encrypting that, and then symmetrically encrypting the message itself.
Digital Signatures
Public key cryptography can also be used to create digital signatures, giving the receiving party assurance of authenticity. Independent of message encryption, Alice’s signature assures Bob that a message is really from her. It also serves as evidence of the communication should Alice deny having sent it. As you’ll recall from Chapter 2, authenticity and non-repudiability are two of the most important security properties for communication, after confidentiality.
Figure 5-2 summarizes the fundamental differences between symmetric encryption on the left, and asymmetric on the right. With symmetric encryption, signing isn’t possible because both communicants know the secret key. The security of asymmetric encryption depends on a private key known only to one communicant, so they alone can use it for signatures. And since verification only requires the public key, no secrets are disclosed in the process.
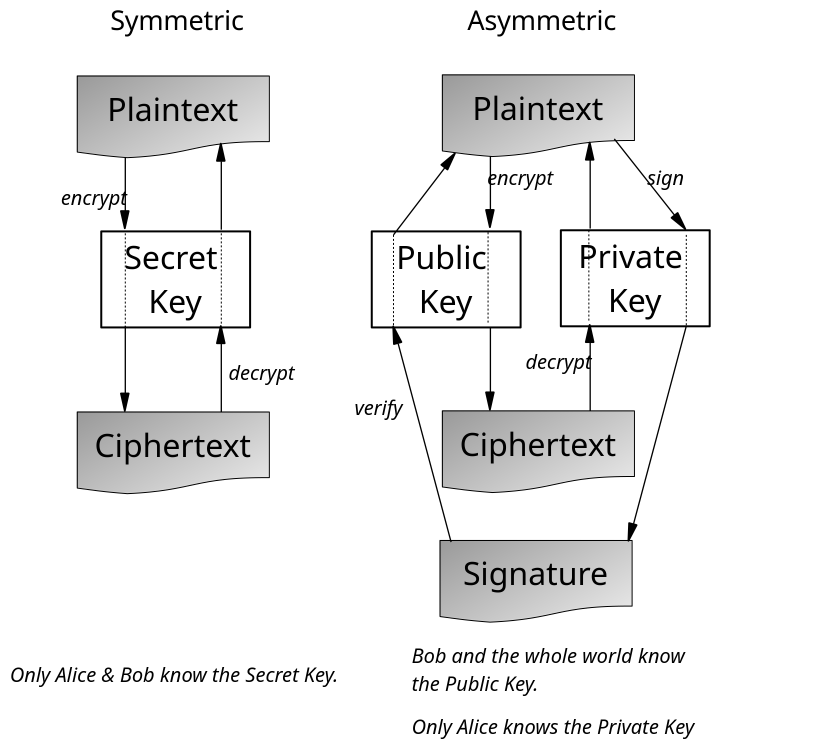
Figure 5-2 A comparison of symmetric and asymmetric cryptography
Let’s walk through an example to illustrate exactly how this works. Alice creates digital signatures using the same key pair that makes public key encryption possible. Because only Alice knows the private key, only she can compute the signature function SA. Bob, or anyone with the public key (and N), can verify Alice’s signature by checking it using the function VA. In other words:
- Alice signs message M to produce a signature S = SA(M).
- Bob verifies that the message M is from Alice by checking if M = VA(S).
There are a few more details to explain so you fully understand how digital signatures work. Since verification only relies on the public key, Bob can prove to a third party that Alice signed a message without compromising Alice’s private key. Also, signing and encrypting of messages are independent: you can do one, the other, or both as appropriate for the application. We won’t tackle the underlying math of RSA in this book, but you should know that the signature and decryption functions (both require the private key) are in fact the same computation, as are the verification and encryption functions (using the public key). To avoid confusion, it’s best to call them by different names according to their purpose.
Digital signatures are widely used to sign digital certificates (the subject of the next section), emails, application code, and legal documents, and to secure cryptocurrencies such as Bitcoin. By convention, digests of messages are signed as a convenience so that one signing operation covers an entire document. Now you can appreciate why a successful preimage attack on a digest function is very bad. If Mallory can concoct a payment agreement with the same message digest, Bob’s promissory note P also serves as a valid signature for it.
Digital Certificates
When I was first learning about the RSA algorithm, I brainstormed with members of the team about possible future applications. The defining advantage of public key crypto was the convenience it offered. It let you use one key for all of your correspondence, rather than managing separate keys for each correspondent, so long as you could announce your public key to the world for anyone to use. But how would one do that?
I came up with an answer in my thesis research, and the idea has since been widely implemented. To promote the new phenomenon of digital public key crypto, we needed a new kind of organization, called a certificate authority** (CA). To get started, a new CA would widely publish its public key. In time, operating systems and browsers would preinstall a trustworthy set of CA root certificates, which contain their public keys.
The CAs collect public keys from applicants, usually for a fee, and then publish a digital certificate for each that lists their name, such as “Alice,” and other details about them, along with their public key. The CA signs a digest of the digital certificate to ensure its authenticity. In theory, an important part of the CA’s service would involve reviewing the application to ensure that it really came from Alice, and people would choose to trust a CA only if they performed this reliably. In practice, it’s very hard to verify identities, especially over the internet, and this has proven problematic.
Once Alice has a digital certificate, she can send people a copy of it whenever she wants to communicate with them. If they trust the CA that issued it, then they have its public key and can validate the digital certificate signature that provides the public key that belongs to “Alice.” The digital certificate is basically a signed message from the CA stating “Alice’s public key is X.” At that point, the recipient can immediately start encrypting messages for Alice, typically beginning by sending their own digital certificate to assure Alice that her message got to the right person. Digital signatures work the same way and are backed by the same digital certificates.
This simplified explanation of digital certificates focuses on how trusted CAs authenticate the association of a name with a private key. In practice, there is more to it; people do not always have unique names, names change, corporations in different states may have the same name, and so on. (Chapter 11 digs into some of these complicating issues in the context of web security.) Today, digital certificates are used to bind keys to various identities, including web server domain names and email addresses, and for a number of specific purposes, such as code signing.
Key Exchange
The first key exchange algorithm was developed by Whitfield Diffie and Martin Hellman shortly before the invention of RSA. To understand the miracle of key exchange, imagine that Alice and Bob have somehow established a communication channel, but they have no prior arrangement of a secret key, or even a CA to trust as a source of public keys. Incredibly, key exchange allows them to establish a secret over an open channel while Mallory observes everything. That this is possible is so counterintuitive that in this case I want to show the math so you can see for yourself how it works.
Fortunately, the math is simple enough and, for small numbers, easy to compute. The only notation that might be unfamiliar to some readers is the suffix (mod p), which means to divide by the integer p to yield the remainder of division. For example, 2^7 (mod 103) is 25, because 128 – 103 = 25.
This is the basis of the Diffie–Hellman key exchange algorithm:
- Alice and Bob openly agree on a prime number p and a random number g (1 < g < p).
- Alice picks a random natural number a (1 < a < p), and sends g^a (mod p) to Bob.
- Bob picks a random natural number b (1 < b < p), and sends g^b (mod p) to Alice.
- Alice computes S = (g^b)^a (mod p) as their shared secret S.
- Bob computes S = (g^a)^b (mod p), getting the same shared secret S as Alice.
Figure 5-3 illustrates a toy example using small numbers to show that this actually works. This example isn’t secure, because an exhaustive search of about 60 possibilities is easy to do. However, the same math works for big numbers, and at the scale of a few hundred digits, it’s wildly infeasible to do such an exhaustive search.
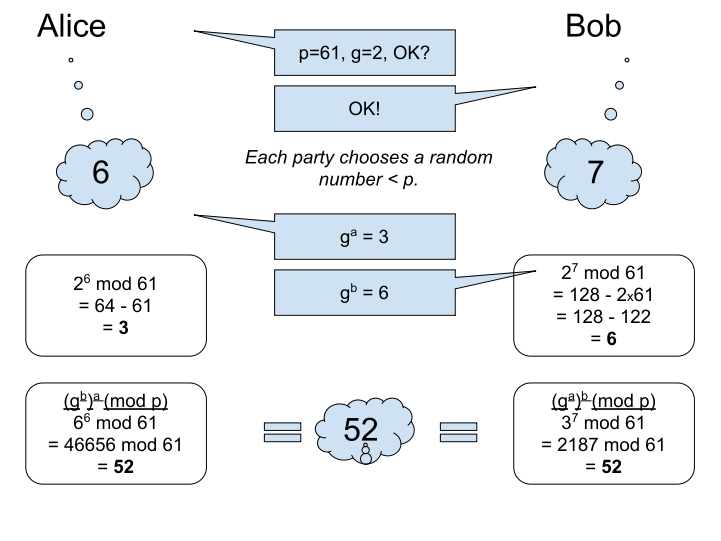
Figure 5-3 Alice and Bob securely choosing a shared secret via key exchange
In this example, chosen to keep the numbers small, by coincidence Alice chooses 6, which happens to equal Bob’s result (g^b). That wouldn’t happen in practice, but of course the algorithm still works and only Alice would notice the coincidence.
It’s important that both parties actually choose secure random numbers from a CSPRNG in order to prevent Mallory possibly guessing their choices. For example, if Bob used a formula to compute his choice from p and g, Mallory might deduce that by observing many key exchanges and eventually mimic it, breaking the secrecy of the key exchange.
Key exchange is basically a magic trick that doesn’t require any deception. Alice and Bob walk in from the wings of the stage with Mallory standing right in the middle. Alice calls out numbers, Bob answers, and after two back-and-forth exchanges Mallory is still clueless. Alice and Bob write their shared secret numbers on large cards, and at a signal hold up their cards to reveal identical numbers representing the agreed secret.
Today, key exchange is critical to establishing a secure communication channel over the internet between any two endpoints. Most applications use elliptic curve key exchange because those algorithms are more performant, but the concept is much the same. Key exchange is particularly handy in setting up secure communication channels (such as with the TLS protocol) on the internet. The two endpoints first use a TCP channel—traffic that Mallory may be observing—then do key exchange to negotiate a secret with the as-yet-unconfirmed opposite communicant. Once they have a shared secret, encrypted communication enables a secure private channel. This is how any pair of communicants can bootstrap a secure channel without a prearranged secret.
Using Crypto
This chapter explained the tools in the crypto toolbox at the “driver’s ed” level. Cryptographically secure random numbers add unpredictability to thwart attacks based on guessing. Digests are a secure way of distilling the uniqueness of data to a corresponding token for integrity checking. Encryption, available in both symmetric and asymmetric forms, protects confidentiality. Digital signatures are a way of authenticating messages. Digital certificates make it easy to share authentic public keys by leveraging trust in CAs. And key exchange rounds out the crypto toolbox, allowing remote parties to securely agree on a secret key via a public network connection.
The comic in Figure 5-4 illustrates the point made by the epigraph that opens this chapter: that well-built cryptography is so strong, the major threat is that it will be circumvented. Perhaps the most important takeaway from this chapter is that it’s crucial to use crypto correctly so you don’t inadvertently provide just such an opening for attack.
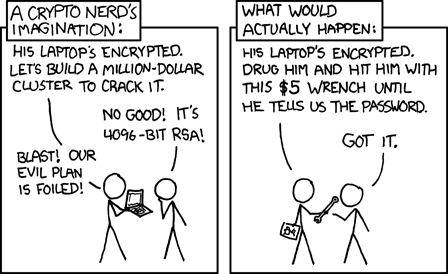
Figure 5-4 Security versus the $5 wrench (courtesy of Randall Munroe, xkcd.com/538)
Crypto can help with many security challenges that arise in the design of your software, or which you identify by threat modeling. If your system must send data over the internet to a partner datacenter, encrypt it (for confidentiality) and digitally sign it (for integrity)—or you could do it the easy way with a TLS secure channel that authenticates the endpoints. Secure digests provide a nifty way to test for data equality, including as MACs, without you needing to store a complete copy of the data. Typically, you will use existing crypto services rather than building your own, and this chapter gives you an idea of when and how to use them, as well as some of the challenges involved in using the technology securely.
Financial account balances and credit card information are clear examples of data you absolutely must protect. This kind of sensitive data flows through a larger distributed system, and even with limited access to the facility, you don’t want someone to be able to physically plug in a network tap and siphon off sensitive data. One powerful mitigation would be to encrypt all incoming sensitive data immediately, when it first hits the frontend web servers. Immediately encrypting credit card numbers with a public key enables you to pass around the encrypted data as opaque blobs while processing the transaction. Eventually, this data reaches the highly protected financial processing machine, which knows the private key and so can decrypt the data and reconcile the transaction with the banking system. This approach allows most application code to safely pass along sensitive data for subsequent processing without risking disclosure itself.
Another common technique is storing symmetrically encrypted data and the secret key in separate locations. For example, consider an enterprise that wants to outsource long-term data storage for backup to a third party. They would hand over encrypted data for safekeeping while keeping the key in their own vault for use, should they need to restore from a backup. In terms of threats, the data storage service is being entrusted to protect integrity (because they could lose the data), but as long as the key is safe and the crypto was done right there is no risk to confidentiality.
These are just a few common usages, and you will find many more ways to use these tools. (Cryptocurrency is one particularly clever application.) Modern operating systems and libraries provide mature implementations of a number of currently viable algorithms so you never have to even think about implementing the actual computations yourself.
Encryption is not a panacea, however, and if attackers can observe the frequency and volume of encrypted data or other metadata, you may disclose some information to them. For example, consider a cloud-based security camera system that captures images when it detects motion in the house. When the family is away, there is no motion, and hence no transmission from the cameras. Even if the images were encrypted, an attacker able to monitor the home network could easily infer the family’s daily patterns and confirm when the house was unoccupied by the drop in camera traffic.
The security of cryptography rests on the known limits of mathematics and the state of the art of digital hardware technology, and both of these are inexorably progressing. Great fame awaits the mathematician who may someday find more efficient computational methods that undermine modern algorithms. Additionally, the prospect of a different kind of computing technology, such as quantum physics, is another potential threat. It is even possible that some powerful nation-state has already achieved such a breakthrough, and is currently using it discreetly, so as not to tip their hand. Like all mitigations, crypto inherently includes trade-offs and unknown risks, but it’s still a great toolbox and set of tools well worth using.