“Low-level programming is good for the programmer’s soul.” —John Carmack

The next few chapters will survey the multitude of coding pitfalls programmers need to be aware of for security reasons, starting with the classics. This chapter covers basic flaws that are common to code that works closer to the machine level. The issues discussed here arise when some code exceeds the capacity of either fixed-size numbers or allocated memory buffers. Modern languages tend to provide higher-level abstractions that insulate code from these perils, but programmers working in these safer languages will still benefit from understanding these flaws, if only to fully appreciate all that’s being done for them, and why it matters.

Languages such as C and C++ that expose these low-level capabilities remain dominant in many software niches, so the potential threats they pose are by no means theoretical. Modern languages such as Python usually abstract away the hardware enough that the issues described in this chapter don’t occur, but the lure of approaching the hardware level for maximum efficiency remains powerful. A few popular languages offer programmers their choice of both worlds. In addition to type-safe object libraries, the Java and C# base types include fixed-width integers, and they have “unsafe” modes that remove many of the safeguards normally provided. Python’s float type, as explained in “Floating-Point Precision Vulnerabilities” on page XX, relies on hardware support and accrues its limitations, which must be coped with.

Readers who never use languages exposing low-level functionality may be tempted to skip this chapter, and can do so without losing the overall narrative of the book. However, I recommend reading through it anyway, as it’s best to understand what protections the languages and libraries you use do or do not provide, and to fully appreciate all that’s being done for you.

Programming closer to the hardware level, if done well, is extremely powerful, but it comes at a cost of increased effort and fragility. In this chapter, we focus on the most common classes of vulnerability specific to coding with lower-level abstractions.

Since this chapter is all about bugs that arise from issues where code is near or at the hardware level, you must understand that the exact results of many of these operations will vary across platforms and languages. I’ve designed the examples to be as specific as possible, but implementation differences may cause varying results—and it’s exactly because computations can vary unpredictably that these issues are easily overlooked and can have an impact on security. The details will vary depending on your hardware, compiler, and other factors, but the concepts introduced in this chapter do apply generally.

Arithmetic Vulnerabilities

Different programming languages variously define their arithmetic operators either mathematically or according to the processor’s corresponding instructions, which, as we shall see shortly, are not quite the same. By low-level, I mean features of programming languages that depend on machine instructions, which requires dealing with the hardware’s quirks and limitations.

Code is full of integer arithmetic. It’s used not only to compute numerical values but also for string comparison, indexed access to data structures, and more. Because the hardware instructions are so much faster and easier to use than software abstractions that handle a larger range of values, they are hard to resist, but with that convenience and speed comes the risk of overflow. Overflow happens when the result of a computation exceeds the capacity of a fixed-width integer, leading to unexpected results, which can create a vulnerability.

Floating-point arithmetic has more range than integer arithmetic, but its limited precision can cause unexpected results too. Even floating-point numbers have limits (for single precision, on the order of 10^38), but when the limit is exceeded, they have the nice property of resulting in a specific value that denotes infinity.

Readers interested in an in-depth treatment of the implementation of arithmetic instructions down to the hardware level can learn more from The Secret Life of Programs by Jonathan E. Steinhart (No Starch Press, 2019).

Fixed-Width Integer Vulnerabilities

At my first full-time job, I wrote device drivers in assembly machine language on minicomputers. Though laughably underpowered by modern standards, minicomputers provided a great opportunity to learn how hardware works, because you could look at the circuit board and see every connection and every chip (which had a modest number of logic gates inside). I could see the registers connected to the arithmetic logic unit (which could perform addition, subtraction, and Boolean operations only) and memory, so I knew exactly how the computer worked. Modern processors are fabulously complicated, containing billions of logic gates, well beyond human understanding by casual observation.

Today, most programmers learn and use higher-level languages that shield them from machine language and the intricacies of CPU architecture. Fixed-width integers are the most basic building blocks of many languages, including Java and C/C++, and if any computation exceeds their limited range, you get the wrong result silently.

Modern processors often have either a 32- or 64-bit architecture, but we can understand how they work by discussing smaller sizes. Let’s look at an example of overflow based on unsigned 16-bit integers. A 16-bit integer can represent any value between 0 and 65,535 (2^16 – 1). For example, multiplying 300 by 300 should give us 90,000, but that number is beyond the range of the fixed-width integer we are using. So, due to overflow, the result we actually get is 24,464 (65,536 less than the expected result).

Some people think about overflow mathematically as modular arithmetic, or the remainder of division (for instance, the previous calculation gave us the remainder of dividing 90,000 by 65,536). Others think of it in terms of binary or hexadecimal truncation, or in terms of the hardware implementation—but if none of these make sense to you, just remember that the results for oversized values will not be what you expect. Since mitigations for overflow will attempt to avoid it in the first place, the precise resulting value is not usually important.

A Quick binary math refresher using 16-bit Architecture

For readers less familiar with binary arithmetic, here is a graphical breakdown of the 300 * 300 computation in the preceding text. Just as decimal numbers are written with the digits zero through nine, binary numbers are written with the digits zero and one. And just as each digit further left in a decimal number represents another tenfold larger position, in binary, the digits double (1, 2, 4, 8, 16, 32, 64, and so on) as they extend to the left. Figure 9-1 shows the 16-bit binary representation of the decimal number 300, with the power-of-two binary digit positions indicated by decimal numbers 0 through 15.

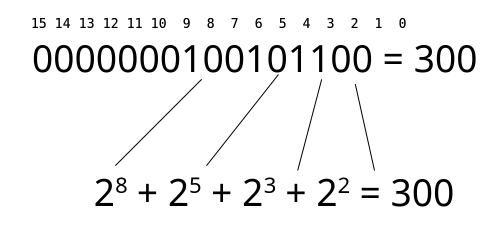
The binary representation is the sum of values shown as powers of two that have a 1 in the corresponding binary digit position. That is, 300 is 2^8 + 2^5 + 2^3 + 2^2 (256 + 32 +8 + 4), or binary 100101100.

Now let’s see how to multiply 300 times itself in binary (Figure 9-2).

Just as you do with decimal multiplication on paper, the multiplicand is repeatedly added, shifted to the position corresponding to a digit of the multiplier. Working from the right, we shift the first instance two digits left because the first 1 has two positions to the right, and so on, with each copy aligned on the right below one of the 1s in the multiplier. The grayed-out numbers extending on the left are beyond the capacity of a 16-bit register and therefore truncated—this is where overflow occurs. Then we just add up the parts, in binary of course, to get the result. The value 2 is 10 (2^1) in binary, so position 5 is the first carry (1 + 1 + 0 = 10): we put down a 0 and carry the 1. That’s how multiplication of fixed-width integers works, and that’s how values get silently truncated.

What’s important here is anticipating the foibles of binary arithmetic, rather than knowing exactly what value results from a calculation—which, depending on the language and compiler, may not be well defined (that is, the language specification refuses to guarantee any particular value). Operations technically specified as “not defined” in a language may seem predictable, but you are on thin ice if the language specification doesn’t offer a guarantee. The bottom line for security is that it’s important to know the language specification and avoid computations that are potentially undefined. Do not get clever and experiment to find a tricky way to detect the undefined result, because with different hardware or a new version of the compiler, your code might stop working.

If you miscompute an arithmetic result your code may break in many ways, and the effects often snowball into a cascade of dysfunction, culminating in a crash or blue screen. Common examples of vulnerabilities due to integer overflow include buffer overflows (discussed in “Buffer Overflow” on page XX), incorrect comparisons of values, situations in which you give a credit instead of charging for a sale, and so on.

It’s best to mitigate these issues before any computation that could go out of bounds is performed, while all numbers are still within range. The easy way to get it right is to use an integer size that is larger than the largest allowable value, preceded by checks ensuring that invalid values never sneak in. For example, to compute 300 * 300, as mentioned earlier, use 32-bit arithmetic, which is capable of handling the product of any 16-bit values. If you must convert the result back to 16-bit, protect it with a 32-bit comparison to ensure that it is in range.

Here is what multiplying two 16-bit unsigned integers into a 32-bit result looks like in C. I prefer to use an extra set of parentheses around the casts for clarity, even though operator precedence binds the casts ahead of the multiplication (I’ll provide a more comprehensive example later in this chapter for a more realistic look at how these vulnerabilities slip in):

uint32_t simple16(uint16_t a, uint16_t b) {
  return ((uint32_t)a) * ((uint32_t)b);
}

The fact that fixed-width integers are subject to silent overflow is not difficult to understand, yet in practice these flaws continue to plague even experienced coders. Part of the problem is the ubiquity of integer math in programming—including its implicit usages, such as pointer arithmetic and array indexing, where the same mitigations must be applied. Another challenge is the necessary rigor of always keeping in mind not just what the reasonable range of values might be for every variable, but also what possible ranges of values the code could encounter, given the manipulations of a wily attacker.

Many times when programming, it feels like all we are doing is manipulating numbers, yet these calculations can be so fragile—but we must not lose sight of the fragility of these calculations.

Floating-Point Precision Vulnerabilities

Floating-point numbers are, in many ways, more robust and less quirky than fixed-width integers. For our purposes, you can think of a floating-point number as a sign bit (for positive or negative numbers), a fraction of a fixed precision, and an exponent of two the fraction is multiplied by. The popular IEEE 754 double-precision specification provides 15 decimal digits (53 binary digits) of precision, and if you exceed its extremely large bounds, you get a signed infinity (or for a few operations, NaN for not a number) instead of truncation to wild values, as you do with fixed-width integers.

Since 15 digits of precision is enough to tally the federal budget of the United States (currently several trillion dollars) in pennies, the risk of loss of precision is rarely a problem. Nonetheless, it does happen silently in the low-order digits, and it can be surprising because the representation of floating-point numbers is binary rather than decimal. For example, since decimal fractions do not necessarily have exact representations in binary, 0.1

• 0.2 will yield 0.30000000000000004—a value that is not equal to 0.3. These kinds of messy results can happen because just as a fraction such as 1/7 is a repeating decimal in base 10, 1/10 repeats infinitely in base 2 (it’s 0.00011001100. . . with 1100 continuing forever), so there will be error in the lowest bits. Since these errors are introduced in the low-order bits, this is called underflow.

Even though underflow discrepancies are tiny proportionally, they can still produce unintuitive results when values are of different magnitudes. Consider the following code written in JavaScript, a language where all numbers are floating point:

var a = 10000000000000000
var b = 2
var c = 1
console.log(((a+b)-c)-a)

Mathematically, the result of the expression in the final line should equal b-c, since the value a is first added and then subtracted. (The console.log function is a handy way to output the value of an expression.) But in fact, the value of a is large enough that adding or subtracting much smaller values has no effect, given the limited precision available, so that when the value a is finally subtracted, the result is zero.

When calculations such as the one in this example are approximate, the error is harmless, but when you need full precision, or when values of differing orders of magnitude go into the computation, then a good coder needs to be cautious. Vulnerabilities arise when such discrepancies potentially impact a security-critical decision in the code. Underflow errors may be a problem for computations such as checksums or for double-entry accounting, where exact results are essential.

For many floating-point computations, even without dramatic underflow like in the example we just showed, small amounts of error accumulate in the lower bits when the values do not have an exact representation. It’s almost always unwise to compare floating-point values for equality (or inequality), since this operation cannot tolerate even tiny differences in computed values. So, instead of (x == y), compare the values within a small range (x > y - delta && x < y + delta) for a value of delta suitable for the application. Python provides the math.isclose helper function that does a slightly more sophisticated version of this test.

When you must have high precision, consider using the super-high-precision floating-point representations (IEEE 754 defines 128- and 256-bit formats). Depending on the requirements of the computation, arbitrary-precision decimal or rational number representations may be the best choice. Libraries often provide this functionality for languages that do not include native support.

Example: Floating-Point Underflow

Floating-point underflow is easy to underestimate, but lost precision has the potential to be devastating. Here is a simple example in Python of an online ordering system’s business logic that uses floating-point values. The following code’s job is to check that purchase orders are fully paid, and if so, approve shipment of the product:

from collections import namedtuple
PurchaseOrder = namedtuple('PurchaseOrder', 'id, date, items')
LineItem = namedtuple('LineItem',
                      ['kind', 'detail', 'amount', 'quantity'],
                      defaults=(1,))
def validorder(po):
    """Returns an error text if the purchase order (po) is invalid,
    or list of products to ship if valid [(quantity, SKU), ...].
    """
    products = []
    net = 0
    for item in po.items:
        if item.kind == 'payment':
            net += item.amount
        elif item.kind == 'product':
            products.append(item)
            net -= item.amount * item.quantity
        else:
            return "Invalid LineItem type: %s" % item.kind
    if net != 0:
        return "Payment imbalance: $%0.2f." % net
    return products

Purchase orders consist of line items that are either product or payment details. The total of payments less credits, minus the total cost of products ordered, should be zero. The payments are already validated beforehand, and let me be explicit about one detail of that process: if the customer immediately cancels a charge in full, both the credit and debit appear as line items without querying the credit card processor, which incurs a fee. Let’s also posit that the prices listed for items are correct.

Focusing on the floating-point math, see how for payment line items the amount is added to net, and for products the amount times quantity is subtracted (these invocations are written as Python doctests, where the \>>> lines are code to run followed by the expected values returned):

>>> tv = LineItem(kind='product', detail='BigTV', amount=10000.00)
>>> paid = LineItem(kind='payment', detail='CC#12345', amount=10000.00)
>>> goodPO = PurchaseOrder(id='777', date='6/16/2019', items=[tv, paid])
>>> validorder(goodPO)
[LineItem(kind='product', detail='BigTV', amount=10000.0, quantity=1)]
>>> unpaidPO = PurchaseOrder(id='888', date='6/16/2019', items=[tv])
>>> validorder(unpaidPO)
'Payment imbalance: $-10000.00.'

The code works as expected, approving the first transaction shown for a fully paid TV and rejecting the order that doesn’t note a payment.

Now it’s time to break this code and “steal” some TVs. If you already see the vulnerability, it’s a great exercise to try and deceive the function yourself. Here is how I got 1,000 TVs for free, with explanation following the code:

>>> fake1 = LineItem(kind='payment', detail='FAKE', amount=1e30)
>>> fake2 = LineItem(kind='payment', detail='FAKE', amount=-1e30)
>>> tv = LineItem(kind='product', detail='BigTV', amount=10000.00, quantity = 1000)
>>> nonpayment = [fake1, tv, fake2]
>>> fraudPO = PurchaseOrder(id='999', date='6/16/2019', items=nonpayment)
>>> validorder(fraudPO)
[LineItem(kind='product', detail='BigTV', amount=10000.0, quantity=1000)]

The trick here is in the fake payment of the outrageous amount 1e30, or 10^30, followed by the immediate reversal of the charge. These bogus numbers get past the accounting check because they sum to zero (10^30 – 10^30). Note that between the canceling debit and the credit is a line item that orders a thousand TVs. Because the first number is so huge, when the cost of the TVs is subtracted, it underflows completely; then, when the credit (a negative number) is added in, the result is zero. Had the credit immediately followed the payment followed by the line item for the TVs, the result would be different and an error would be correctly flagged.

To give you a more accurate feel for underflow—and more importantly, to show how to gauge the range of safe values to make the code secure—we can drill in a little deeper. The choice of 10^30 for this attack was arbitrary, and this trick works with numbers as low as about 10^24, but not 10^23. The cost of 1,000 TVs at $10,000 each is $10,000,000, or 10^7. So with a fake charge of 10^23, the value 10^7 starts to change the computation a little, corresponding to about 16 digits of precision (23 – 7). The previously mentioned 15 digits of precision was a safe rule-of-thumb approximation (the binary precision corresponds to 15.95 decimal digits) that’s useful because most of us think naturally in base 10, but since the floating-point representation is actually binary, it can differ by a few bits.

With that reasoning in mind, let’s fix this vulnerability. If we want to work in floating point, then we need to constrain the range of numbers. Assuming a minimum product cost of $0.01 (10^–2) and 15 digits of precision, we can set a maximum payment amount of $10^13 (15 – 2), or $10 trillion. This upper limit avoids underflow, though in practice, a smaller limit corresponding to a realistic maximum order amount would be best.

Using an arbitrary-precision number type avoids underflow: in Python, that could be the native integer type, or fractions.Fraction. Higher-precision floating-point computation will prevent this particular attack but would still be susceptible to underflow with more extreme values. Since Python is dynamically typed, when the code is called with values of these types, the attack fails. But even if we had written this code with one of these arbitrary precision types and considered it safe, if the attacker managed to sneak in a float somehow, the vulnerability would reappear. That’s why doing a range check—or, if the caller cannot be trusted to present the expected type, converting incoming values to safe types before computing—is important.

Example: Integer Overflow

Fixed-width integer overflow vulnerabilities are often utterly obvious in hindsight, and this class of bugs has been well known for many years. Yet experienced coders repeatedly fall into the trap, whether because they don’t believe the overflow can happen, because they misjudge it as harmless, or because they don’t consider it at all. The following example shows the vulnerability in a larger computation to give you an idea of how these bugs can easily slip in. In practice, vulnerable computations tend to be more involved, and the values of variables harder to anticipate, but for explanatory purposes, this simple code will make it easy to see what’s going on.

Consider this straightforward payroll computation formula: the number of hours worked times the rate of pay gives the total dollars of pay. This simple calculation will be done in fractional hours and dollars, which gives us full precision. On the flip side, with rounding, the details get a little complicated, and as will be seen, integer overflow easily happens.

Using 32-bit integers for exact precision, we compute dollar values in cents (units of $0.01), and hours in thousandths (units of 0.001 hours), so the numbers do get big. But as the highest possible 32-bit integer value, UINT32_MAX, is over 4 billion (2^32 – 1), we assume we’ll be safe by the following logic: company policy limits paid work to 100 hours per week (100,000 in thousandths), so at an upper limit of $400/hour (40,000 cents), that makes a maximum paycheck of 4,000,000,000 (and $40,000 is a nice week’s pay).

Here is the computation of pay in C, with all variables and constants defined as uint32_t values:

if (millihours > max_millihours      // 100 hours max
   || hourlycents > max_hourlycents) // $400/hour rate max
  return 0;
return (millihours * hourlycents + 500) / 1000; // Round to $.01

The if statement, which returns an error indication for out-of-range parameters, is an essential guard to prevent overflow in the computation that follows.

The computation in the return statement deserves explanation. Since we are representing hours in thousandths, we must divide the result by 1,000 to get the actual pay, so we first add 500 (half of the divisor) for rounding. A trivial example confirms this: 10 hours (10,000) times $10.00/hour (1,000) equals 10,000,000; add 500 for rounding, giving 10,000,500; and divide by 1,000, giving 10,000 or $100.00, the correct value. Even at this point, you should consider this code fragile, to the extent that it flirts with the possibility of truncation due to fixed-width integer limitations.

So far the code works fine for all inputs, but suppose management has announced a new overtime policy. We need to modify the code to add 50 percent to the pay rate for all overtime hours (any hours worked after the first 40 hours). Further, the percentage should be a parameter, so management can easily change it later.

To add the extra pay for overtime hours, we introduce overtime_percentage. The code for this isn’t shown, but its value is 150, meaning 150 percent of normal pay for overtime hours. Since the pay will increase, the $400/hour limit won’t work anymore, because it won’t be low enough to prevent integer overflow. But that pay rate was unrealistic as a practical limit anyhow, so let’s halve it, just to be safe, and say $200/hour is the top pay rate:

if (millihours > max_millihours      // 100 hours max
    || hourlycents > max_hourlycents) // $200/hour rate max
  return 0;
if (millihours > overtime_millihours) {
  overage_millihours = millihours - overtime_millihours;
  overtimepay = (overage_millihours * hourlycents * overtime_percentage
                   + 50000) / 100000;
  basepay = (overtime_millihours * hourlycents + 500) / 1000;
  return basepay + overtimepay;
}
else
  return (millihours * hourlycents + 500) / 1000;

Now, we check if the number of hours exceeds the overtime pay threshold (40 hours), and if not, the same calculation applies. In the case of overtime, we first compute overage_millihours as the hours (in thousandths) over 40.000. For those hours, we multiply the computed pay by the overtime_percentage (150). Since we have a percentage (two digits of decimal fraction) and thousandths of hours (three digits of decimals), we must divide by 100,000 (five zeros) after adding half that for rounding. After computing the base pay on the first 40 hours, without the overtime adjustment, the code sums the two to calculate the total pay. For efficiency, we could combine these similar computations, but the intention here is for the code to structurally match the computation, for clarity.

This code works most of the time, but not always. One example of an odd result is that 60.000 hours worked at $50.00/hour yields $2,211.51 in pay (it should be $3,500.00). The problem is with the multiplication by overtime_percentage (150) which easily overflows with a number of overtime hours at a good rate of pay. In integer arithmetic, we cannot precompute 150/100 as a fraction—as an integer that’s just 1—so we have to do the multiplication first.

To fix this code, we could replace (X*150)/100 with (X*3)/2, but that ruins the parameterization of the overtime percentage and wouldn’t work if the rate changed to a less amenable value. One solution that maintains the parameterization would be to break up the computation so that the multiplication and division use 64-bit arithmetic, downcasting to a 32-bit result:

if (millihours > max_millihours      // 100 hours max
   || hourlycents > max_hourlycents) // $200/hour rate max
  return 0;
if (millihours > overtime_millihours) {
  overage_millihours = millihours - overtime_millihours;
  product64 = overage_millihours * hourlycents;
  adjusted64 = (product64 * overtime_percentage + 50000) / 100000;
  overtimepay = ((uint32_t)adjusted64 + 500) / 1000;
  return basepay + overtimepay;
}
else
  return (millihours * hourlycents + 500) / 1000;

For illustrative purposes, the 64-bit variables include that designation in their names. We could also write these expressions with a lot of explicit casting, but it would get long and be less readable.

The multiplication of three values was split up to multiply two of them into a 64-bit variable before overflow can happen; once upcast, the multiplication with the percentage is 64-bit and will work correctly. The resultant code is admittedly messier, and comments to explain the reasoning would be helpful. The cleanest solution would be to upgrade all variables in sight to 64-bit at a tiny loss of efficiency. Such are the trade-offs involved in using fixed-width integers for computation.

Safe Arithmetic

Integer overflow is more frequently problematic than floating-point underflow, because it can generate dramatically different results, but we can by no means safely ignore floating-point underflow, either. Since by design compilers do arithmetic in ways that potentially diverge from mathematical correctness, developers are responsible for dealing with the consequences. Once aware of these problems, you can adopt several mitigation strategies to help avoid vulnerabilities.

Avoid tricky coding to handle potential overflow problems, because any mistakes will be hard to find by testing and represent potentially exploitable vulnerabilities. Additionally, a trick might work on your machine but not be portable to other CPU architectures or different compilers. Here is a summary of how to do these computations safely:

• Type conversions potentially can truncate or distort results, just as calculations can.
• Where possible, constrain inputs to the computation to ensure that all possible values are representable.
• Use a larger fixed-size integer to avoid possible overflow; check that the result is within bounds before converting it back to a smaller-sized integer.
• Remember that intermediate computed values may overflow, causing a problem, even if the final result is always within range.
• Use extra care when checking the correctness of arithmetic in and around security-sensitive code.

If the nuances of fixed-width integer and floating-point computations still feel arcane, watch them closely and expect surprises in what might seem like elementary calculations. Once you know they can be tricky, a little testing with some ad hoc code in your language of choice is a great way to get a feel for the limits of the basic building blocks of computer math.

Once you have identified code at risk of these sort of bugs, make test cases that invoke calculations with extreme values for all inputs, then check the results. Well-chosen test cases can detect overflow problems, but a limited set of tests is not proof that the code is immune to overflow.

Fortunately, more modern languages, such as Python, increasingly use arbitrary-precision integers and are not generally subject to these problems. Getting arithmetic computation right begins with understanding precisely how the language you use works in complete detail. You can find an excellent reference with details for several popular languages at the memorable URL floating-point-gui.de, which provides in-depth explanation and best-practice coding examples.

Memory Access Vulnerabilities

The other vulnerability class we’ll discuss involves improper memory access. Direct management of memory is powerful and potentially highly efficient, but it comes with the risk of arbitrarily bad consequences if the code gets anything wrong.

Most programming languages offer fully managed memory allocation and constrain access to proper bounds, but for reasons of efficiency or flexibility, or sometimes because of the inertia of legacy, other languages (predominantly C and C++) make the job of memory management the responsibility of the programmer. When programmers take this job on—even experienced programmers—they can easily get it wrong, especially as the code gets complicated, creating serious vulnerabilities. And as with the arithmetic flaws described earlier, the great danger is when a violation of memory management protocol goes uncaught and continues to happen silently.

In this section, the focus is on the security aspects of code that directly manages and accesses memory, absent built-in safeguards. Code examples will use the classic dynamic memory functions of the original C standard library, but these lessons apply generally to the many variants that provide similar functionality.

Memory Management

Pointers allow direct access to memory by its address, and they are perhaps the most powerful feature of the C language. But just like when wielding any power tool, it’s important to use responsible safety precautions to manage the attendant risk. Software allocates memory when needed, works within its available bounds, and releases it when no longer needed. Any access outside of this agreement of space and time will have unintended consequences, and that’s where vulnerabilities arise.

The C standard library provides dynamic memory allocation for large data structures, or when the size of a data structure cannot be determined at compile time. This memory is allocated from the heap—a large chunk of address space in the process used to provide working memory. C programs use malloc(3) to allocation memory, and when it’s no longer needed, they release each allocation for reuse by calling free(3). There are many variations on these allocation and deallocation functions; we will focus on these two for simplicity, but the ideas should apply anytime code is managing memory directly.

Access after memory release can easily happen when lots of code shares a data structure that eventually gets freed, but copies of the pointer remain behind and get used in error. After the memory gets recycled, any use of those old pointers violates memory access integrity. On the flip side, forgetting to release memory after use risks exhausting the heap over time and running out of memory. The following code excerpt shows the basic correct usage of heap memory:

uint8_t *p;
// Don't use the pointer before allocating memory for it.
p = malloc(100); // Allocate 100 bytes before first use.
p[0] = 1;
p[99] = 123 + p[0];
free(p);          // Release the memory after last use.
// Don't use the pointer anymore.

This code accesses the memory between the allocation and deallocation calls, inside the bounds of allotted memory.

In actual use, the allocation, memory access, and deallocation can be scattered around the code, making it tricky to always do this just right.

Buffer Overflow

A buffer overflow (or, alternatively, buffer overrun) occurs when code accesses a memory location outside of the intended target buffer. It’s important to be very clear about the meaning, because the terminology is confusing. Buffer is a general term for any data in memory: data structures, character strings, arrays, objects, or variables of any type. Access is a catch-all term for reading or writing memory. That means a buffer overflow involves reading or writing outside of the intended memory region, even though “overflow” more naturally describes the act of writing. While the effects of reading and writing differ fundamentally, it’s useful to think of them together to understand the problem.

Buffer overflows are not exclusive to heap memory, but can occur with any kind of variable, including static allocations and local variables on the stack. All of these potentially modify other data in memory in arbitrary ways. Unintended writes out of bounds could change just about anything in memory, and clever attackers will refine such an attack to try to cause maximum damage. In addition, buffer overflow bugs may read memory unexpectedly, possibly leaking information to attackers or otherwise causing the code to misbehave.

Don’t underestimate the difficulty and importance of getting explicit memory allocation, access within bounds, and release of unused storage exactly right. Simple patterns of allocation, use, and release are best, including exception handling to ensure that the release is never skipped. When allocation by one component hands off the reference to other code, it’s critical to define responsibility for subsequently releasing the memory to one side of the interface or the other.

Finally, be cognizant that even in a fully range-checked, garbage-collected language, you can still get in trouble. Any code that directly manipulates data structures in memory can make errors equivalent to buffer overflow issues. Consider, for example, manipulating a binary data structure, such as a TCP/IP packet in a Python array of bytes. Reading the contents and making modifications involves computing offsets into data and can be buggy, even if access outside the array does not occur.

Example: Memory Allocation Vulnerabilities

Let’s look at an example showing the dangers of dynamic memory allocation gone wrong. I’ll make this example straightforward, but in actual applications the key pieces of code are often separated, making these flaws much harder to see.

A Simple Data Structure

This example uses a simple C data structure representing a user account. The structure consists of a flag that’s set if the user is an admin, a user ID, a username, and a collection of settings. The semantics of these fields don’t matter to us, except if the isAdmin field is nonzero, as this confers unlimited authorization (making this field an attractive target for attack):

#define MAX_USERNAME_LEN 39
#define SETTINGS_COUNT 10
typedef struct {
  bool isAdmin;
  long userid;
  char username[MAX_USERNAME_LEN + 1];
  long setting[SETTINGS_COUNT];
} user_account;

Here’s a function that creates these user account records:

user_account* create_user_account(bool isAdmin,
                                  const char* username) {
  user_account* ua;
  if (strlen(username) > MAX_USERNAME_LEN)
    return NULL;
  ua = malloc(sizeof (user_account));
  if (NULL == ua) {
    fprintf(stderr, "malloc failed to allocate memory.");
    return NULL;
  }
  ua->isAdmin = isAdmin;
  ua->userid = userid_next++;
  strcpy(ua->username, username);
  memset(&ua->setting, 0, sizeof ua->setting);
  return ua;
}

The first parameter specifies whether the user is an admin or not. The second parameter provides a username, which must not exceed the specified maximum length. A global counter (userid\_next, declaration not shown) provides sequential unique IDs. The values of all the settings are set to zero initially, and the code returns a pointer to the new record unless an error causes it to return NULL instead. Note that the code checks the length of the username string before the allocation, so that allocation happens only when the memory will get used.

Writing an Indexed Field

After we’ve created a record, the values of all the settings can be set using the following function:

bool update_setting(user_account* ua,
                    const char *index, const char *value) {
  char *endptr;
  long i, v;
  i = strtol(index, &endptr, 10);
  if (*endptr)
    return false; // Terminated other than at end of string.
  if (i >= SETTINGS_COUNT)
    return false;
  v = strtol(value, &endptr, 10);
  if (*endptr)
    return false; // Terminated other than at end of string.
  ua->setting[i] = v;
  return true;
}

This function takes an index into the settings and a value as decimal number strings. After converting these to integers, it stores the value as the indexed setting in the record. For example, to assign setting 1 the value 14, we would invoke the function update\_setting(ua, "1", "14").

The function strtol converts the strings to integer values. The pointer that strtol sets (endptr) tells the caller how far it parsed; if that isn’t the null terminator, the string wasn’t a valid integer and the code returns an error. After ensuring that the index (i) does not exceed the number of settings, it parses the value (v) in the same way, and stores the setting’s value in the record.

Buffer Overflow Vulnerability

All this setup is simplicity itself, though C tends to be verbose. Now let’s cut to the chase. There’s a bug: there is no check for a negative index value. If an attacker can manage to get this function called as update\_setting(ua, "-12", "1") they can become an admin. This is because the assignment into settings accesses 48 bytes backward into the record, because each item is of type long, which is 4 bytes. Therefore, the assignment writes the value 1 into the isAdmin field, granting excess privileges.

In this case, the fact that we allowed negative indexing within a data structure caused an unauthorized write to memory that violated a security protection mechanism. You need to watch out for many variations on this theme, including indexing errors due to missing limit checks or arithmetic errors such as overflow. Sometimes, a bad access out of one data structure can modify other data that happens to be in the wrong place.

The fix is to prevent negative index values from being accepted, which limits write accesses to the valid range of settings. The following addition to the if statement rejects negative values of i, closing the loophole:

  if (i < 0 || i >= SETTINGS_COUNT)

The additional i < 0 condition will now reject any negative index value, blocking any unintended modification by this function.

Leaking Memory

Even once we’ve fixed the negative index overwrite flaw, there’s still a vulnerability. The documentation for malloc(3) warns, with underlining, “The memory is not initialized.” This means that the memory could contain anything, and a little experimentation does show that leftover data appears in there, so recycling the uninitialized memory represents a potential leak of private data.

Our create\_user\_account function does write data to all fields of the structure, but it still leaks bytes that are in the data structure as recycled memory. Compilers usually align field offsets that allow efficient writing: on my 32-bit computer, field offsets are a multiple of 4 (4 bytes of 8 bits is 32), and other architectures perform similar alignments. The alignment is needed because writing a field that spans a multiple-of-4 address (for example, writing 4 bytes to address 0x1000002) requires two memory accesses. So in this example, after the single-byte Boolean isAdmin field at offset 0, the userid field follows at offset 4, leaving the three intervening bytes (offsets 1–3) unused. Figure 9-3 shows the memory layout of the data structure in graphical form.

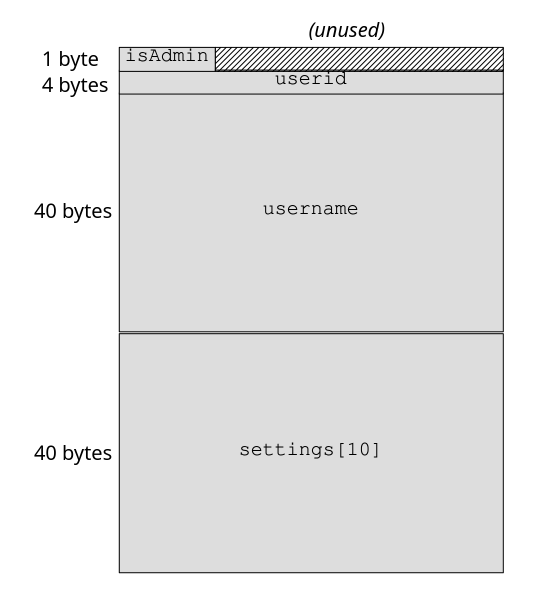
Additionally, the use of strcpy for the username leaves another chunk of memory in its uninitialized state. This string copy function stops copying at the null terminator, so the 5-byte string in this example only modifies the first 6 bytes, leaving 34 bytes of whatever malloc happened to grab for us. The point of all this is that the newly allocated structure contains residual data which may leak unless every byte is overwritten.

Mitigating the risk of these inadvertent memory leaks isn’t hard, but you must diligently overwrite all bytes of data structures that could be exposed. You shouldn’t attempt to anticipate precisely how the compiler might allocate field offsets, because this could vary over time and across platforms. Instead, the easiest way to avoid these issues is to zero out buffers once allocated unless you can otherwise ensure they are fully written. Remember that even if your code doesn’t use sensitive data itself, this memory leak path could expose other data anywhere in the process.

Generally speaking, you should avoid using strcpy to copy strings because there are so many ways to get it wrong. The strncpy function both fills unused bytes in the target with zeros and protects against overflow with strings that exceed the buffer size. However, strncpy does not guarantee that the resultant string will have a null terminator. This is why it’s essential to allocate the buffer to be of size MAX_USERNAME_LEN + 1, ensuring that there is always room for the null terminator. Another option is to use the strlcpy function, which does ensure null termination; however, for efficiency, it does not zero-fill unused bytes. As this example shows, when you handle memory directly there are many factors you must deal with carefully.

Now that we’ve covered the mechanics of memory allocation and seen what vulnerabilities look like in a constructed example, let’s consider a more realistic case. The following example is based on a remarkable security fiasco from several years ago that compromised a fair share of the world’s major web services.

Case Study: Heartbleed

In early April 2014, headlines warned of a worldwide disaster narrowly averted as major operating system platforms and websites rolled out coordinated fixes, hastily arranged in secret, in an attempt to minimize their exposure as details of the newly identified security flaw became public. Heartbleed made news not only as “the first security bug with a cool logo,” but because it revealed a trivially exploitable hole in the armor of any server deploying the popular OpenSSL TLS library.

What follows is an in-depth look at one of the scariest security vulnerabilities of the decade, and it should provide you with context for how serious mistakes can be. The purpose of this detailed discussion is to illustrate how bugs managing dynamically allocated memory can become devastating vulnerabilities. As such, I have simplified the code and some details of the complicated TLS communication protocol to show the crux of the vulnerability. Conceptually, this corresponds directly with what actually occurred, but with fewer moving parts and much simpler code.

Heartbleed is a flaw in the OpenSSL implementation of the TLS Heartbeat Extension, proposed in 2012 with RFC 6520. This extension provides a low-overhead method for keeping TLS connections alive, saving clients from having to re-establish a new connection after a period of inactivity. The so-called heartbeat itself is a round-trip message exchange consisting of a heartbeat request, with a payload of between 16 and 16,384 (2^14) bytes of arbitrary data, echoed back as a heartbeat response containing the same payload. Figure 9-4 shows the basic request and response messages of the protocol.

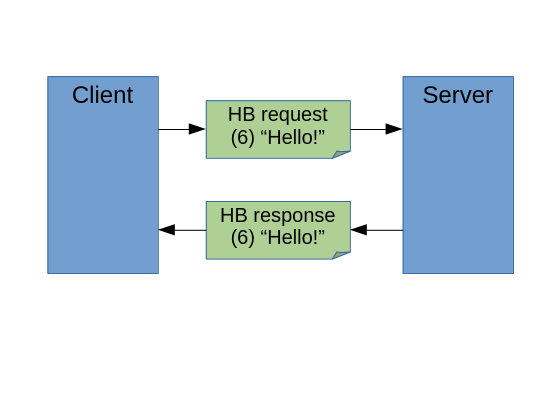
Having downloaded an HTTPS web page, the client may later send a heartbeat request on the connection to let the server know that it wants to maintain the connection. In an example of normal use, the client might send the 16-byte message “Hello Heartbeat!” comprising the request, and the server would respond by sending the same 16 bytes back. (That’s how it’s supposed to work, at least.) Now let’s look at the Heartbleed bug.

The critical flaw occurs in malformed heartbeat requests that provide a small payload yet claim a larger payload byte count. To see exactly how this works, let’s first look at the internal structure of one of the simplified heartbeat messages that the peers exchange. All of the code in this example is in C:

typedef struct {
  HeartbeatMessageType type;
  uint16_t payload_length;
  char bytes[0]; // Variable-length payload & padding
} hbmessage;

The data structure declaration hbmessage shows the three parts of one of these heartbeat messages. The first field is the message type, indicating whether it’s a request or response. Next is the length in bytes of the message payload, called payload\_length. The third field, called bytes, is declared as zero-length, but is intended to be used with a dynamic allocation that adds the appropriate size needed.

A malicious client might attack a target server by first establishing a TLS connection to it, and then sending a 16-byte heartbeat request with a byte count of 16,000. Here’s what that looks like as a C declaration:

typedef struct {
  HeartbeatMessageType type = heartbeat_request;
  uint16_t payload_length = 16000;
  char bytes[16] = {"Hello Heartbeat!"};
} hbmessage;

The client sending this is lying: the message says its payload is 16,000 bytes long but the actual payload is only 16 bytes. To understand how this message tricks the server, look at the C code that processes the incoming heartbeat request message:

hbmessage *hb(hbmessage *request, int *message_length) {
  int response_length = request->payload_length+sizeof(hbmessage);
  hbmessage* response = malloc(response_length);
  response->type = heartbeat_response;
  response->payload_length = request->payload_length;
  memcpy(&response->bytes, &request->bytes,
         response->payload_length);
  *message_length = response_length;
  return response;
}

The hb function gets called with two parameters: the incoming heartbeat request message and a pointer named message\_length, which stores the length of the response message that the function returns. The first two lines compute the byte length of the response as response\_length, then a memory block of that size gets allocated as response. The next two lines fill in the first two values of the response message: the message type, and its payload\_length.

Next comes the fateful bug. The server needs to send back the message bytes received in the request, so it copies the data from the request into the response. Because it trusts the request message to have accurately reported its length, the function copies 16,000 bytes—but since there are only 16 bytes in the request message, the response includes thousands of bytes of internal memory contents. The last two lines store the length of the response message and then return the pointer to it.

Figure 9-5 illustrates this exchange of messages, detailing how the preceding code leaks the contents of process memory. To make the harm of the exploit concrete, I’ve depicted a couple of additional buffers, containing secret data, already sitting in memory in the vicinity of the request buffer. Copying 16,000 bytes from a buffer that only contained a 16-byte payload—illustrated here by the overly large dotted-line region— results in the secret data ending up in the response message, which the server sends to the client.

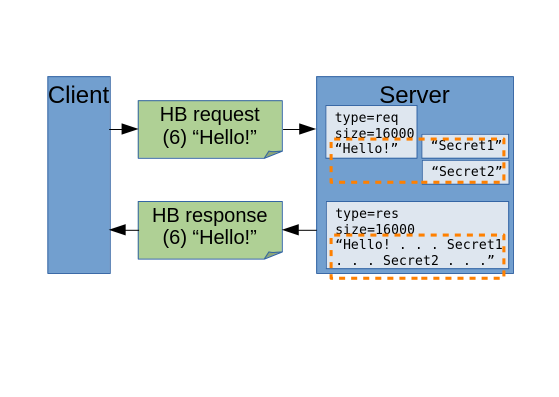
This flaw is tantamount to configuring your server to provide an anonymous API that snapshots and sends out thousands of bytes of working memory to all callers—a complete breach of memory isolation, exposed to the internet. It should come as no surprise that web servers using HTTPS security have any number of juicy secrets in working memory. According to the discoverers of the Heartbleed bug, they were able to easily steal from themselves “the secret keys used for our X.509 certificates, user names and passwords, instant messages, emails and business critical documents and communication.” Since exactly what data leaked depended on the foibles of memory allocation, the ability of attackers exploiting this vulnerability to repeatedly access server memory eventually yielded all kinds of sensitive data.

The fix was straightforward in hindsight: anticipate “lying” heartbeat requests that ask for more payload than they provide, and, as the RFC explicitly specifies, ignore them. Thanks to Heartbleed, the world learned how dependent so many servers were on OpenSSL, and how few volunteers were laboring on the critical software that so much of the internet’s infrastructure depended on. The bug is typical of why many security flaws are difficult to detect, because everything works flawlessly in the case of well-formed requests, and only malformed requests that well-intentioned code would be unlikely to ever make cause problems. Furthermore, the leaked server memory in heartbeat responses causes no direct harm to the server: only by careful analysis of the excessive data disclosure does the extent of the potential damage become evident.

As arguably one of the most severe security vulnerabilities discovered in recent years, Heartbleed should serve as a valuable example of the nature of security bugs, and how small flaws can result in a massive undermining of our systems’ security. From a functional perspective, one could easily argue that this is a minor bug: it’s unlikely to happen, and sending back more payload data than the request provided seems, at first glance, utterly harmless.

HeartBleed explanation (https://xkcd.com/1354/)

Heartbleed is an excellent object lesson in the fragility of low-level languages. Small errors can have massive impact. A buffer overflow potentially exposes high-value secrets if they happen to be lying around in memory at just the wrong location. The design (protocol specification) anticipated this very error by directing that heartbeat requests with incorrect byte lengths should be ignored, but without explicit testing, nobody noticed the vulnerability for over two years.

This is just one bug in one library. How many more like it are still out there now?